Abdul Bari Algorithms - Recurrence Relation and Master's Theorem for Dividing Functions
Discusses the recurrence relation for dividing functions, which decrease the number of subproblems by dividing


Dividing Recurrence Relation 1
function test(n) {
if (n > 1) {
console.log(n);
test(n / 2);
}
}When a function takes a parameter n, it can make it smaller by either subtracting like or dividing like or
Amount of work is
Recurrence Relation Dividing
Tree Method
1 unit of work per level, k steps, which is how many levels
Assume
Simplify to
Then simplify again to , which is the number of levels
Since there’s one unit of work per level, the number of levels is the total units of work
Substitution Method
Original Equation
Plug in
Generalized to
Assume
and
Answer
Dividing Recurrence Relation 2
Recurrence Relation
Tree Method
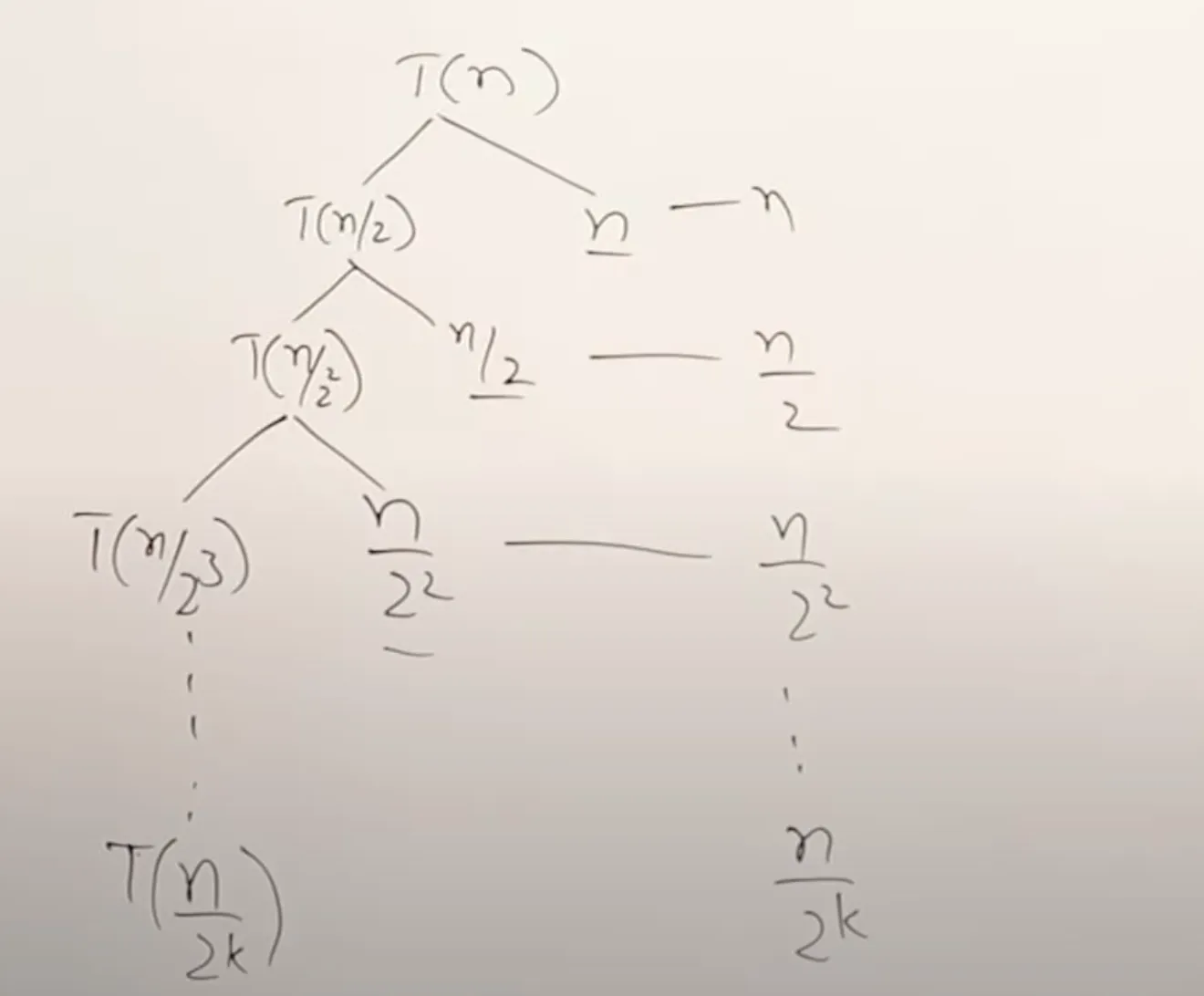
Each level does amount of work
So for each level,
This simplifies to n * 1
so answer is
Substitution Method
Assume
Answer
Dividing Recurrence Relation 3
function test(n) {
if (n > 1) {
for (let i = 0; i < n; i++) {
console.log(n);
}
test(n / 2);
test(n / 2);
}
}The recurrence relation is
Tree Method
Each row adds up to amount of work
2nd row as 2 s
3rd row has 4 s
each row is
How many rows are there? and in each row how much work is being done?
so n work being done k times
Assume
So total amount of work is
Substitution Method
Plug in
Substitute into the original equation
Repeat for k times
Assume
Master’s Theorem for Dividing 1
Assume and
Case 1
if then
Case 2
if
Case 2.1
if then
Case 2.2
if then
Case 2.3
if then
Case 3
if
Case 3.1
if then
Case 3.2
if then
Examples
Case 1
Example 1
,
which is bigger than so it is case 1
Example 2
, ,
which is bigger than k (1) so case 1
Example 3
>
Also case 1, so
Example 4
>
Still case 1, so
Example 5
>
case 1, so
Case 2
Example 1
and
They’re equal so case 2
No in , which is just (original formula
so
Example 2
and
They’re equal so case 2
so
Example 3
and
They’re equal so case 2
so
Example 4
and
They’re equal so case 2
so
Example 5
Remember is the same as
and
They’re equal so case 2
In this case since it’s in denominator
So case 2.2
Example 6
Remember is the same as
and
They’re equal so case 2
In this case since it’s in denominator
So case 2.3
or
Case 3
Example 1
<
So case 3.1
So
Example 2
<
So case 3.1, take the entire
So
Example 3
If log is in denominator, then case 3.2
<
So case 3.2, so just take
So
Master’s Theorem for Dividing 2
Case 1 Examples
->
->
->
->
->
Case 2
->
->
->
->
->
->
->
Case 3
->
->
->
->
->
Root Function (Recurrence Relation)
function test(n){
if(n>2) {
stmt
test(Math.sqrt(n))
}
Continue for k times
Assume n is in powers of 2
Assume
and
and