Heap, Heap Sort, Heapify, and Priority Queues

Heap - Heap Sort - Heapify - Priority Queues

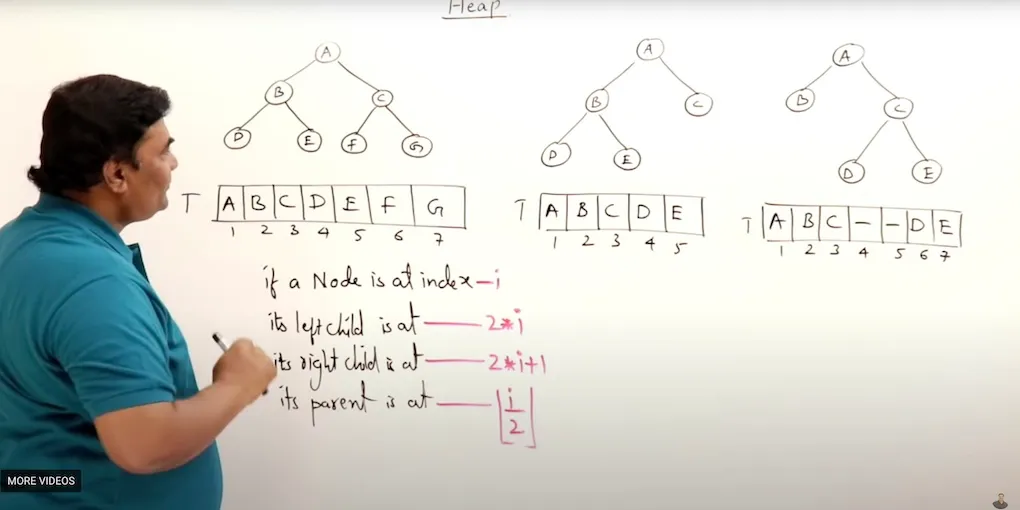
Array Representation of Binary Tree

[a, b, c, d, e, f, g]

You can store a binary tree as an array.

When storing a binary tree we need to store the elements as well as the relationship between the elements.

Binary Tree Representation Formula

If a node is at index i:

• The left child is at index 2*i+1
• The right child is at index 2*i+2
• The parent is at Math.floor((i-1)/2)

Examples

What is the left child of b which is at index 1?

The left child index is 2*1+1 = 3, and the element at index 3 is d.

What is the right child of b which is at index 1?

The right child index is 2*1+2 = 4, and the element at index 4 is e.

What is the parent of f which is at index 5?

The parent index is Math.floor((5-1)/2) = 2, and the element at index 2 is c.

You can also think about filling them level by level.

Missing Nodes at the End

[a, b, c, d, e]

Leave out the missing elements at the end.

Gaps

Imagine filling it level by level, but leave a gap:

[a, b, c, null, null, d, e]

Children of b are missing, so leave a gap.

Complete Binary Tree

Full Binary Tree

A full binary tree has the maximum number of nodes for its height. You can’t add another node without increasing its height.

The number of nodes in a full binary tree with height $h$ is $2^{h+1}-1$.

Complete Binary Tree

When represented as an array, a complete binary tree doesn’t have any gaps.

Complete Binary Tree Example

Its array representation is [a, b, c, d, e, f, g] and it has no gaps, so it’s a complete binary tree.

Non-Complete Binary Tree

Its array representation is [a, b, c, null, null, d, e] and has gaps, so it is not a complete binary tree.

Every full binary tree is also a complete binary tree.

Heap

A heap is a complete binary tree.

Max heap is a complete binary tree where every node is greater than or equal to its descendants. The largest node is the root.

Min heap is a complete binary tree where every node is smaller than its descendants. The smallest node is the root.

Insert

We want to insert an element into a max heap:

Array representation = [50, 30, 20, 15, 10, 8, 16]

Let’s try inserting 60.

The root should have the largest element so the root should be 60.

We need to maintain completeness while inserting.

We start by inserting 60 at the end of the array, which corresponds to the bottom left element of the complete binary tree: [50, 30, 20, 15, 10, 8, 16, 60]

Swap upward with parents until the correct height:

[60, 50, 20, 30, 10, 8, 16, 15]

We add the new element as a leaf, then adjust its ancestors upward.

How much time does it take? The maximum number of swaps equals the height of a complete binary tree, which is $O(log(n))$.

Delete

You should only delete the root element.

Imagine picking an apple at the top of a pyramid at the supermarket.

We delete 50:

[50, 30, 20, 15, 10, 8, 16]

Remove 50, and replace with the last element of the binary tree, 16:

Now we adjust the elements from the root towards the leaf, maintaining the complete binary property.

Check 16’s child elements. Which child is greater? 30, so swap with 30:

Check 16’s child elements. Which child is greater? 15, so swap with 15:

Heap Sort

If you keep deleting, the next largest element goes to the top in max heap. In min heap the next smallest comes to the top.

After deleting the largest element, we have a “free space” at the end.

Before deleting:

[50, 30, 20, 15, 10, 8, 16]

After deleting:

[30, 16, 20, 15, 10, 8, null]

We can keep the element we removed at the end of the array to preserve it:

[30, 16, 20, 15, 10, 8, 50]

Let’s delete again, removing 30:

[20, 16, 10, 15, 8, null, 50]

But we preserve 30 at the end of the heap:

[20, 16, 10, 15, 8, 30, 50]

We can see that we’re sorting the array by deleting the largest element, and filling it in at the free space at the end of the new array.

How to Do Heap Sort

Heap sort has two steps:

1. Create a heap from an array by inserting the elements one by one
2. Delete the elements one by one

Heap Sort Example

Create Heap

These are the unsorted set of elements: [10, 20, 15, 30, 40]

Assume 10 is the root of the heap:

Now insert second element 20:

[10, 20]

Compare with ancestor, 20 is greater, so swap:

[20, 10]

Now insert the third element 15:

Compare with parent, it’s smaller, so we don’t need to adjust.

[20, 10, 15]

Now insert the fourth element 30:

[20, 10, 15, 30]

Adjust the element by comparing to parent, greater than 10 so swap:

Adjust the element by comparing to parent, greater than 20 so swap:

Sorted, so now elements are [30, 20, 15, 10].

Now insert the fifth element 40:

[30, 20, 15, 10, 40]

Compare with parent and swap upward:

Swap upward again:

Now the heap is [40, 30, 15, 10, 20].

Every element was inserted at the next free space and moved upward.

We inserted n elements, each element was moved up the height of the binary tree.

So we have $n$ elements moved up by height $log(n)$, so time complexity to build heap is $n\ast log(n)$.

Delete All Elements

[40, 20, 15, 10, 20]

40 gets deleted and 20 takes its place at the root:

[20, 30, 15, 10]

Now we need to adjust the binary tree by swapping downward.

Check which of the children of 20 is greater, then swap.

30 is greater, so swap 20 and 30:

Compare 20 with 10, don’t need to swap.

[30, 20, 15, 10] [40], keeping 40 at the end.

30 gets deleted and the last element 10 takes its place at the root:

[10, 20, 15]

Now adjust by comparing with children.

Swap 10 with 20:

Now this is in max heap form, so we stop.

20, 10, 15 and our reserved elements [30, 40]

Now we delete 20 and replace with 15:

We don’t need to adjust since the child is smaller.

15, 10 is the new heap and our reserved elements [20, 30, 40]

Now delete 15 and replace with 10:

We don’t need to adjust since there’s just one element.

Our heap is [10] and our reserved elements at the end are [15, 20, 30, 40].

So together now the array is sorted: 10, 15, 20, 30, 40

Heapify

Heapify is a procedure for creating a heap from a binary tree.

Array representation: [10, 20, 15, 12, 40, 25, 18]

It’s similar to creating a heap from scratch. Before we saw when creating a heap from scratch, we insert from the root and adjust down. However, in heapify we adjust upwards.

We start with a complete binary tree, but it isn’t a max heap.

In heapify we go from right to left, instead of left to right in creating a heap.

When going from right to left, we adjust downward, similar to deletion.

Start with element 18 and look at its descendants. It’s a leaf with no children, so alone it is a heap. Continuing on we see the same with 25, 40, and 12.

We get to 15 and adjust downwards. We compare it to its children and swap. Which child is greater? 25 is greater, so we swap with 15. 25 goes up and 15 goes down in its place:

Now we’re on 20. Compare with children. 40 is greater, so swap 20 with 40:

Now we get to the first element, the root.

We compare 40 with its children, and swap 10 with 40:

We continue heapifying down, and check 10’s children. 20 is greater so we swap with 10:

What is the time taken by heapify? $O(n)$

The earlier procedure for creating a heap was $O(n\ast log(n))$, which is slower than heapify.

Priority Queue

Elements have priority, and are inserted and deleted based on that priority.

Elements with the highest priority are removed first.

In a numeric array, the priority is based on the number itself.

We can say that the highest priority is the smallest number, or we can say the largest number has the highest priority, depending on the use case. We can do either method of priority.

The time for insert or delete for a regular array is $O(n)$ because we have to shift the elements.

The time for insert or delete for a priority queue is $O(log(n))$ which is faster than a normal array.