Recurrence Relation and Master's Theorem for Dividing Functions

Dividing Recurrence Relation 1

function test(n) {
  if (n > 1) {
    console.log(n);
    test(n / 2);
  }
}

When a function takes a parameter n, it can make it smaller by either subtracting like $n-1$ or dividing like $n/2$ or $\sqrt{n}$.

Amount of work is $T(n)=T(n/2)+1$

Recurrence Relation Dividing

$T(n)=\{\begin{array}{ll}1& \text{when }n=1\\ 2T(n/2)+n& \text{when }n>1\end{array}$

Tree Method

Each level does 1 unit of work across $k$ levels.

Assuming $\frac{n}{2^k}=1$, we get $n=2^k$, which simplifies to $k={\log }_2(n)$.

Since there’s one unit of work per level, the total work equals the number of levels: $O(\log n)$.

Substitution Method

Starting with $T(n)=T(n/2)+1$, we substitute repeatedly:

$T(n/2)=T(n/2^2)+1$ $T(n)=[T(n/2^2)+1]+1=T(n/2^2)+2$ $T(n)=T(n/2^3)+3$

Generalizing to $k$ iterations: $T(n)=T(n/2^k)+k$

Assuming $\frac{n}{2^k}=1$, we get $n=2^k$ and $k=\log n$.

Substituting: $T(n)=T(1)+\log n=1+\log n$

Answer: $O(\log n)$

Dividing Recurrence Relation 2

Recurrence Relation

$T(n)=\{\begin{array}{ll}1& \text{when }n=1\\ T(n/2)+n& \text{when }n>1\end{array}$

Tree Method

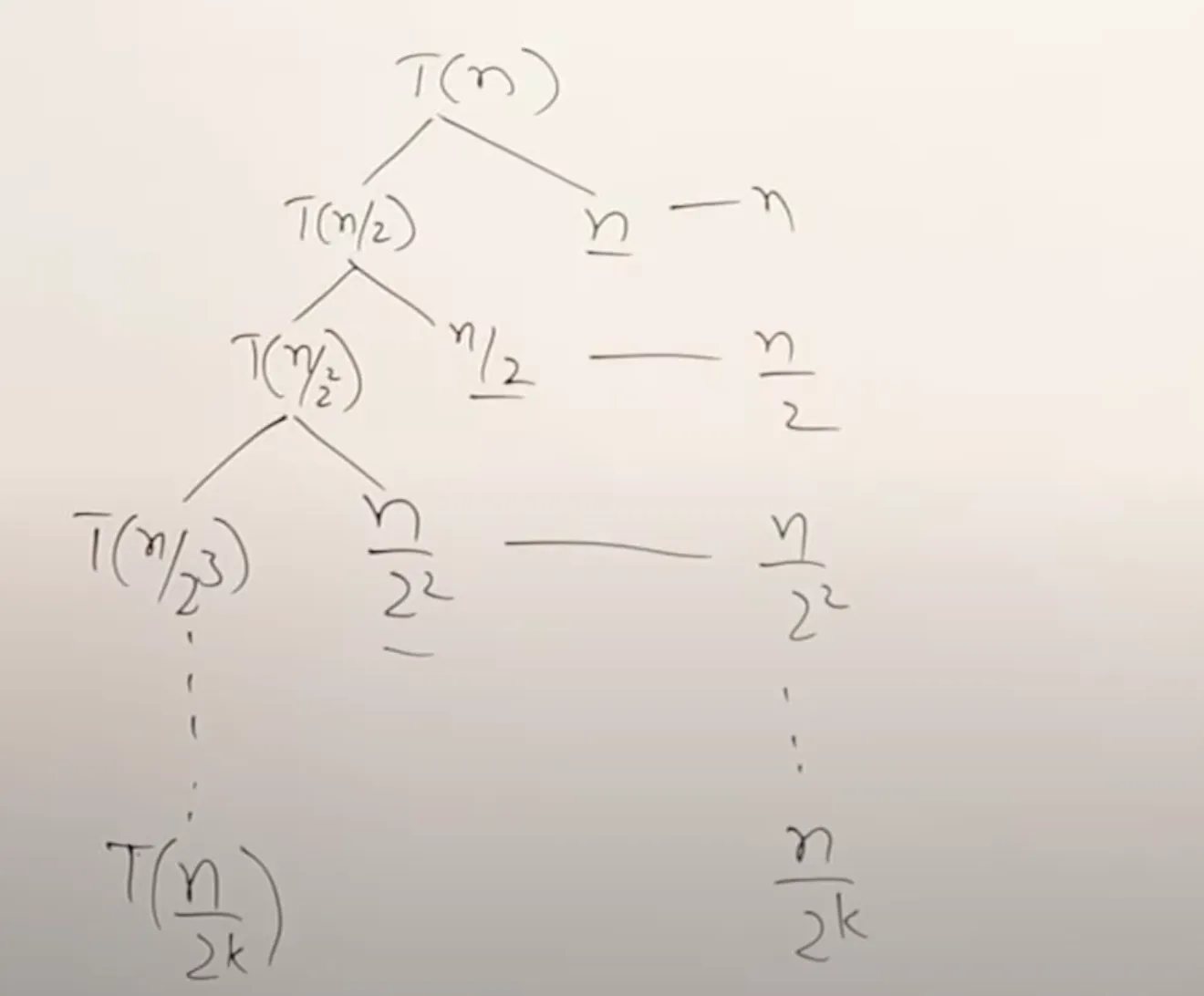
Each level does $\frac{n}{2^k}$ amount of work.

So for each level, $n+\frac{n}{2}+\frac{n}{2^2}+\frac{n}{2^3}+...+\frac{n}{2^k}$

$n\sum _{i=0}^k\frac{1}{2^i}$

This simplifies to n * 1

so answer is $O(n)$

Substitution Method

Starting with $T(n)=T(n/2)+n$:

$T(n)=[T(n/2^2)+n/2]+n=T(n/2^2)+n/2+n$ $T(n)=T(n/2^3)+n/2^2+n/2+n$ $T(n)=T(n/2^k)+n/2^{k-1}+\cdots +n/2+n$

Assuming $\frac{n}{2^k}=1$, we get $n=2^k$ and $k=\log n$.

$T(n)=T(1)+n\left[\frac{1}{2^{k-1}}+\frac{1}{2^{k-2}}+\cdots +\frac{1}{2}+1\right]=1+n\cdot 2=1+2n$

Answer: $O(n)$

Dividing Recurrence Relation 3

function test(n) {
  if (n > 1) {
    for (let i = 0; i < n; i++) {
      console.log(n);
    }
    test(n / 2);
    test(n / 2);
  }
}

The recurrence relation is $T(n)=2T(n/2)+n$

$T(n)=\{\begin{array}{ll}1& \text{when }n=1\\ 2T(n/2)+n& \text{when }n>1\end{array}$

Tree Method

Each row adds up to $n$ amount of work: the 2nd row has two $n/2$s, the 3rd row has four $n/4$s, and so on. Each row contributes $\frac{n}{2^k}\cdot 2^k=n$ work.

Assuming $\frac{n}{2^k}=1$, we get $n=2^k$ and $k=\log n$.

Since $n$ work is done across $\log n$ levels, the total work is $n\cdot \log n$.

Substitution Method

Starting with $T(n)=2T(n/2)+n$, we substitute $T(n/2)=2T(n/2^2)+n/2$:

$T(n)=2[2T(n/2^2)+n/2]+n=4T(n/2^2)+2n$

Continuing for $k$ iterations: $T(n)=2^k\cdot T(n/2^k)+kn$

Assuming $T(n/2^k)=T(1)$, we get $\frac{n}{2^k}=1$ and $k=\log n$.

Master’s Theorem for Dividing Functions

For recurrences of the form $T(n)=a\cdot T(n/b)+f(n)$ where $a\ge 1$, $b>1$, and $f(n)=O(n^k\cdot {\log }^{p}n)$:

Case 1: ${\log }_b(a)>k$

Then $T(n)=O(n^{{\log }_b(a)})$

Case 2: ${\log }_b(a)=k$

• Case 2.1: If $p>-1$, then $T(n)=O(n^k\cdot {\log }^{p+1}n)$
• Case 2.2: If $p=-1$, then $T(n)=O(n^k\cdot \log (\log n))$
• Case 2.3: If $p<-1$, then $T(n)=O(n^k)$

Case 3: ${\log }_b(a)<k$

• Case 3.1: If $p\ge 0$, then $T(n)=O(n^k\cdot {\log }^{p}n)$
• Case 3.2: If $p<0$, then $T(n)=O(n^k)$

Examples

Case 1

Example 1: $T(n)=2T(n/2)+1$

Here $a=2$, $b=2$, and $f(n)=O(1)=O(n^0\cdot \log (n{)}^0)$, so $k=0$ and $p=0$.

Since ${\log }_2(2)=1>k=0$, this is case 1. Answer: $O(n)$

Example 2: $T(n)=4T(n/2)+n$

Here ${\log }_2(4)=2$, $k=1$, $p=0$. Since ${\log }_2(4)=2>k=1$, this is case 1. Answer: $O(n^2)$

Example 3: $T(n)=8T(n/2)+n$

Here ${\log }_2(8)=3>k=1$. Case 1, so $O(n^3)$

Example 4: $T(n)=8T(n/2)+n^2$

Here ${\log }_2(8)=3>k=2$. Still case 1, so $O(n^3)$

Example 5: $T(n)=9T(n/3)+1$

Here ${\log }_3(9)=2>k=0$. Case 1, so $O(n^2)$

Case 2

Example 1: $T(n)=2T(n/2)+n$

Here ${\log }_2(2)=1$ and $k=1$, so they’re equal (case 2). Since $f(n)=n$ has no $\log (n)$ term, $p=0$. Answer: $O(n\log n)$

Example 2: $T(n)=4T(n/2)+n^2$

Here ${\log }_2(4)=2=k$, so case 2 with $p=0$. Answer: $O(n^2\log n)$

Example 3: $T(n)=4T(n/2)+n^2\log n$

Here ${\log }_2(4)=2=k$, so case 2 with $p=1$. Answer: $O(n^2{\log }^{2}n)$

Example 4: $T(n)=8T(n/2)+n^3$

Here ${\log }_2(8)=3=k$, so case 2 with $p=0$. Answer: $O(n^3\log n)$

Example 5: $T(n)=2T(n/2)+\frac{n}{\log n}$

Note that $\frac{n}{\log n}=n\cdot \log (n{)}^{-1}$. Here ${\log }_2(2)=1=k$ and $p=-1$ (in denominator), so case 2.2. Answer: $O(n\log (\log n))$

Example 6: $T(n)=2T(n/2)+\frac{n}{{\log }^{2}n}$

Here ${\log }_2(2)=1=k$ and $p=-2$ (in denominator), so case 2.3. Answer: $O(n)$

Case 3

Example 1: $T(n)=T(n/2)+n^2$

Here ${\log }_2(1)=0<k=2$, so case 3.1. Answer: $O(n^2)$

Example 2: $T(n)=T(n/2)+n^2\log n$

Here ${\log }_2(1)=0<k=2$, so case 3.1—take the entire $f(n)$. Answer: $O(n^2\log n)$

Example 3: $T(n)=T(n/2)+\frac{n^3}{\log n}$

Here ${\log }_2(1)=0<k=3$. Since log is in the denominator, this is case 3.2—just take $n^k$. Answer: $O(n^3)$

Master’s Theorem Summary Tables

Case 1: ${\log }_b(a)>k$

Case 2: ${\log }_b(a)=k$

Case 3: ${\log }_b(a)<k$

Root Function (Recurrence Relation)

function test(n){
  if(n>2) {
    stmt
    test(Math.sqrt(n))
  }
}

$T(n)=\{\begin{array}{ll}1& \text{when }n=2\\ T(\sqrt{n})+1& \text{when }n>2\end{array}$

Expanding by substitution:

$T(n)=T(n^{1/2})+1=T(n^{1/4})+2=T(n^{1/8})+3$

Generalizing to $k$ iterations: $T(n)=T(n^{1/2^k})+k$

Let $n=2^m$. Then $T(2^m)=T(2^{m/2^k})+k$.

Assuming $T(2^{m/2^k})=T(2)$, we need $m/2^k=1$, so $m=2^k$ and $k={\log }_2(m)$.

Since $n=2^m$, we have $m={\log }_2(n)$, giving us $k=\log (\log n)$.

Answer: $O(\log (\log n))$