Time Complexity Analysis

Introduction to algorithms

Algorithms vs programs

Priori vs posteriori analysis

See my detailed notes on a posteriori vs a priori analysis.

A priori analysis is theoretical, hardware independent, and language independent. We analyze time and space as mathematical functions.

A posteriori analysis measures actual execution time and memory usage on real hardware.

Algorithm characteristics

Input

Algorithms can take zero or more inputs.

Output

Algorithms must generate some result. If an algorithm doesn’t produce output, it’s not useful. Even a void function should have some observable effect, like modifying a variable.

Definiteness

Everything should be unambiguous and clear. If you can’t describe the problem to a human, you don’t understand it well enough to write an algorithm.

For example, you can’t pass an imaginary number like $\sqrt{-1}$ without specifying how to handle it.

Finiteness

Algorithms must terminate at some point. A web server that runs indefinitely is a program, not an algorithm. Programs may use algorithms internally.

Effectiveness

Don’t include unnecessary steps. In chemistry, you wouldn’t boil a chemical and then not use it in the experiment.

How to write and analyze algorithms

Swapping two numbers

Here’s pseudocode for swapping two values:

function swap(a, b) {
  tmp = a;
  a = b;
  b = tmp;
}

Criteria for analyzing algorithms

Time and space are the most important criteria.

Time: How long will the algorithm take to run?

Space: How much memory does the algorithm need?

Other characteristics may matter in specific contexts:

• Network traffic: How much data is sent over the network?
• Power: How much energy does the algorithm consume? (Important for mobile devices)
• CPU registers: For low-level software, you may need to know hardware details.

Time analysis

Every “simple” statement takes one “unit” of time. A procedure with 3 simple statements takes 3 units of time, written as $f(n)=3$.

This is a constant value. It doesn’t matter what input you give it.

For simplicity, we usually say y = 3*a + 6*b is just 1 unit of time. It’s not necessary to count every operation.

Space analysis

What’s the space complexity of the swap function? It uses 3 variables always, regardless of input, so $s(n)=3$ which is constant.

Each variable is one “unit” of space.

Frequency count method

The time taken by an algorithm can be determined by assigning one “unit” of time for each statement. If a statement repeats, the frequency of execution determines the time.

Sum of elements in array

function sumArray(nums) {
  sum = 0;
  for (i = 0; i < nums.length; i++) {
    sum = sum + nums[i];
  }
  return sum;
}

Time complexity: Given an array of length n, the sum operation runs n times, so the algorithm takes $O(n)$ time. We call this “order of n.”

Space complexity: We have variables sum, i, and nums. The array nums has n units of space, while i and sum each have 1 unit. Since nums dominates, the space complexity is $O(n)$.

Matrix addition

function addMatrix(a, b) {
  for (i = 0; i < a.length; i++) {
    for (j = 0; j < a[0].length; j++) {
      c[i][j] = a[i][j] + b[i][j];
    }
  }
}

Time complexity: Two nested for loops, each running n times. That’s n procedures executing n times, giving us $O(n^2)$.

Space complexity: Three matrices (a, b, c) and two scalar variables (i, j).

Time complexity patterns

How do we analyze time complexity for different code patterns?

Normal for loops

The statement executes n times, so it’s $O(n)$:

for (i = 0; i < n; i++) {
  stmt();
}

Decrementing for loop

Even though i decrements, the statement still executes n times, so it’s $O(n)$:

for (i = n; i > 0; i--) {
  stmt();
}

Increment by two

for (i = 0; i < n; i += 2) {
  stmt();
}

This executes n/2 times. It’s still $O(n)$ because constants are dropped.

Nested for loops

for (i = 0; i < n; i++) {
  for (j = 0; j < n; j++) {
    stmt();
  }
}

Each loop executes n times, so the statement runs $n\times n$ times, giving $O(n^2)$.

Dependent for loops

What if the inner loop depends on the outer loop?

for (i = 0; i < n; i++) {
  for (j = 0; j < i; j++) {
    stmt();
  }
}

Let’s trace the values:

How many times does stmt execute? This is equivalent to $1+2+3+...+n$.

Using the integer sum formula:

$f(n)=\frac{n(n+1)}{2}=\frac{n^2+n}{2}$

This simplifies to $O(n^2)$ because we only care about the highest power.

Non-linear loop termination

p = 0;
for (i = 1; p <= n; i++) {
  p = p + i;
  stmt();
}

Let’s trace the values:

Using the integer sum formula, $p=\frac{k(k+1)}{2}$.

The loop stops when $p>n$:

$\frac{k(k+1)}{2}>n$

This simplifies to $k^2>n$, so $k>\sqrt{n}$.

The time complexity is $O(\sqrt{n})$.

Multiply i value

for (i = 1; i < n; i = i * 2) {
  stmt();
}

The pattern is $i=2^{k-1}$. The loop stops when $i\ge n$:

$2^k=n$

$k={\log }_{2}n$

The time complexity is $O(\log n)$.

Divide i value

for (i = n; i >= 1; i = i / 2) {
  stmt();
}

The sequence is $n,\frac{n}{2},\frac{n}{4},\frac{n}{8},...$

The loop stops when $i<1$:

$\frac{n}{2^k}=1$

$n=2^k$

$k={\log }_{2}n$

The time complexity is $O(\log n)$.

While loops and conditionals

We can analyze functions with while loops and if statements by tracing values:

while (m != n) {
  if (m > n) {
    m = m - n;
  } else {
    n = n - m;
  }
}

With input 16, it runs 7 times (16/2 - 1). The time complexity is $O(n)$.

Classes of functions

These are listed in increasing order of growth:

Sample values

Exponential functions grow much faster. When n gets large, $n^{100}$ will always be less than $2^n$.

Image credit: Cmglee

Asymptotic notation

Big O ($O$) - Upper bound

$f(n)=O(g(n))$ means there exist positive constants c and k such that $0\le f(n)\le c\cdot g(n)$ for all $n\ge k$.

If you graph the bounding function, your function’s value is always less than the Big O upper bound.

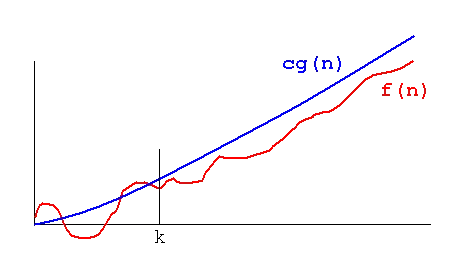
Source: NIST

For example, if $f(n)=2n+3$, then $10n>2n+3$ for large n, so $f(n)=O(n)$.

Use the closest function for the upper bound. Even though $n^2$ could be an upper bound for a linear function, it’s less useful.

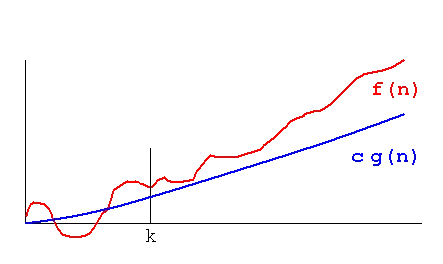
Big Omega ($\Omega$) - Lower bound

Similar to Big O, but your function is always greater than the omega function.

$f(n)=\Omega (g(n))$ means there exist positive constants c and k such that $f(n)\ge c\cdot g(n)$ for all $n\ge k$.

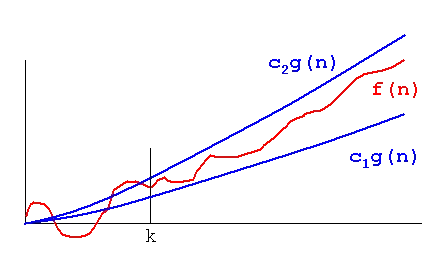
Theta ($\Theta$) - Tight bound

$f(n)=\Theta (g(n))$ means there exist positive constants $c_1$, $c_2$, and k such that $c_1\cdot g(n)\le f(n)\le c_2\cdot g(n)$ for all $n\ge k$.

For $f(n)=2n+3$:

$1\cdot n\le 2n+3\le 5\cdot n$

So $f(n)=\Theta (n)$.

Since this is a tight bound, you can’t use $\Theta (n^2)$ for a linear function.

Properties of asymptotic notation

General property

If $f(n)=O(g(n))$, then $a\cdot f(n)=O(g(n))$ for any constant a.

Example: $f(n)=2n^2+5$ is $O(n^2)$, and $7(2n^2+5)=14n^2+35$ is also $O(n^2)$.

Reflexive property

$f(n)=O(f(n))$

Example: $n^2=O(n^2)$

Transitive property

If $f(n)=O(g(n))$ and $g(n)=O(h(n))$, then $f(n)=O(h(n))$.

If g(n) is an upper bound for f(n), and h(n) is an upper bound for g(n), then h(n) is also an upper bound for f(n).

Symmetric property (Theta only)

If $f(n)=\Theta (g(n))$, then $g(n)=\Theta (f(n))$.

Transpose symmetric property (O and Omega)

If $f(n)=O(g(n))$, then $g(n)=\Omega (f(n))$.

Example: $n=O(n^2)$ and $n^2=\Omega (n)$

Combining functions

If $f(n)=O(g(n))$ and $d(n)=O(e(n))$:

• Addition: $f(n)+d(n)=O(\max (g(n),e(n)))$
• Multiplication: $f(n)\cdot d(n)=O(g(n)\cdot e(n))$

Comparing functions

To determine which function is the upper bound, we can sample values or apply logarithms.

For $n^2$ vs $n^3$:

Applying log to both sides:

$\log (n^2)$ vs $\log (n^3)$

$2\log (n)$ vs $3\log (n)$

We can see that $2\log (n)\le 3\log (n)$, so $n^2=O(n^3)$.

Logarithm rules

• $\log (a\cdot b)=\log (a)+\log (b)$
• $\log (\frac{a}{b})=\log (a)-\log (b)$
• $\log (a^b)=b\cdot \log (a)$
• $a^{{\log }_c(b)}=b^{{\log }_c(a)}$
• If $a^b=n$, then $b={\log }_a(n)$

Best, worst, and average case

Linear search

Given a list [8, 6, 12, 5, 9, 7, 4, 3, 16, 18] and searching for 7:

Linear search starts at the first element and checks each one, moving left to right.

Best case: Element is at the first index. Time is $O(1)$.

Worst case: Element is at the last index or not present. Time is $O(n)$.

Average case: We sum the time for all possible positions and divide by the number of cases.

If the element is at position 1, we do 1 comparison. At position 2, 2 comparisons. And so on.

Total comparisons: $1+2+3+...+n$

Using the integer sum formula: $\frac{n(n+1)}{2}$

Dividing by n cases: $\frac{n+1}{2}$

This is the average case time.

Note on notation

Don’t confuse best/worst/average case with Big O/Omega/Theta. Best case can be expressed using any of these notations:

• Best case = 1
• Best case = $O(1)$
• Best case = $\Omega (1)$
• Best case = $\Theta (1)$

Binary search

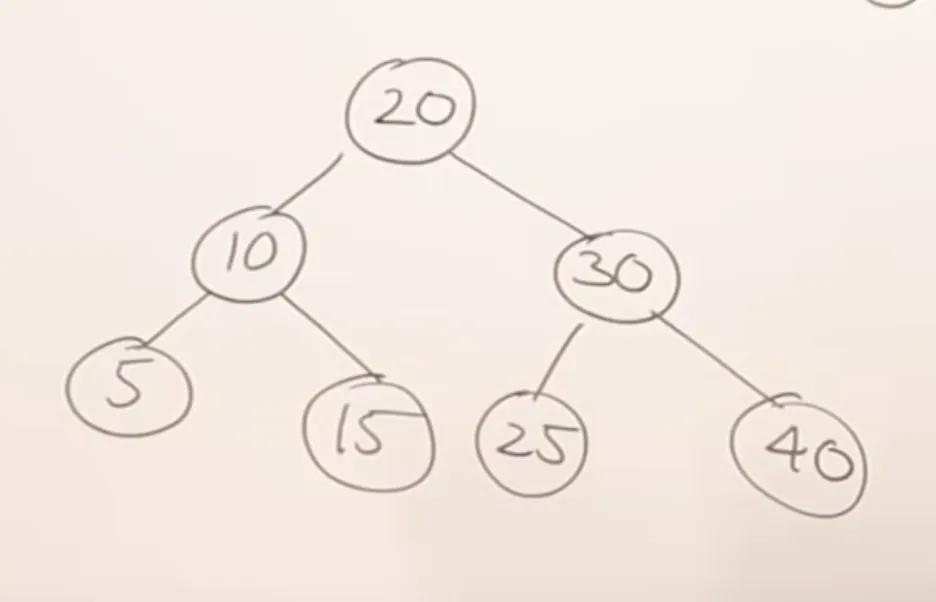
If searching for 15, start at root 20. Is 15 smaller? Yes, go left. Check 10. Is 15 larger? Yes, go right.

Best case: Element is the root. Time is $O(1)$.

Worst case: Element is a leaf. Time is the height of the tree, which is $O(\log n)$ for a balanced tree.

Unbalanced binary search tree

A binary tree can be unbalanced. This left-skewed tree has height n.

Best case is still $O(1)$ when the element is at the root.

However, worst case is $O(n)$ because the height is n, compared to $O(\log n)$ for a balanced tree.